Windows下使用laradock作为开发环境
本文共 1400 字,大约阅读时间需要 4 分钟。
Windows下使用laradock作为开发环境
关于laradock
- laradock是laravel官方维护的一个用于php开发docker集成环境 预先打包的Docker镜像,所有配置官方基本提供了。
- Laradock是在laravel社区众所周知的,因为这个项目最开始只关注在Docker上运行的laravel项目。后来,由于PHP社区的大量使用,它开始支持比如Symfony、CodeIgniter、WordPress、Drupal等其他的PHP项目。
我的个人用例
- 即使在windows下它依然是我平台开发的主要环境,基于学习docker都有比较好的帮助,我也是去年开始学习并使用docker。并在实际的业务场景中基于laradock给客户部署过一套php相关的项目,也基于客户内网部署过一套docker lnmp环境 ,使用和了解它,使我大大缩减了大部分部署相关环境消耗的时间:
开始安装docker
- 安装完成并开启虚拟化
启动异常问题
- 关闭USE 我们使用git工具作为命令行操作面板
- 登录docker账号 这个在官网注册一个
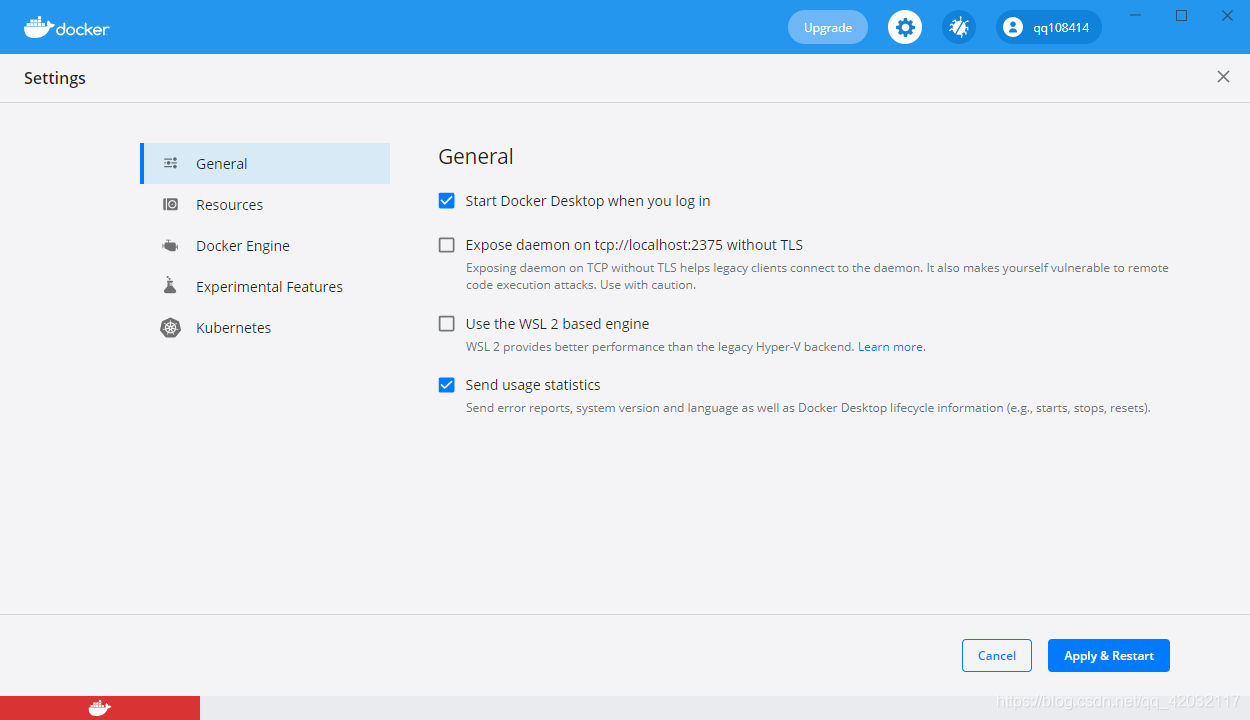
- 设置一个镜像源 有服务器的同学可以在自己服务器平台创建一个 或者
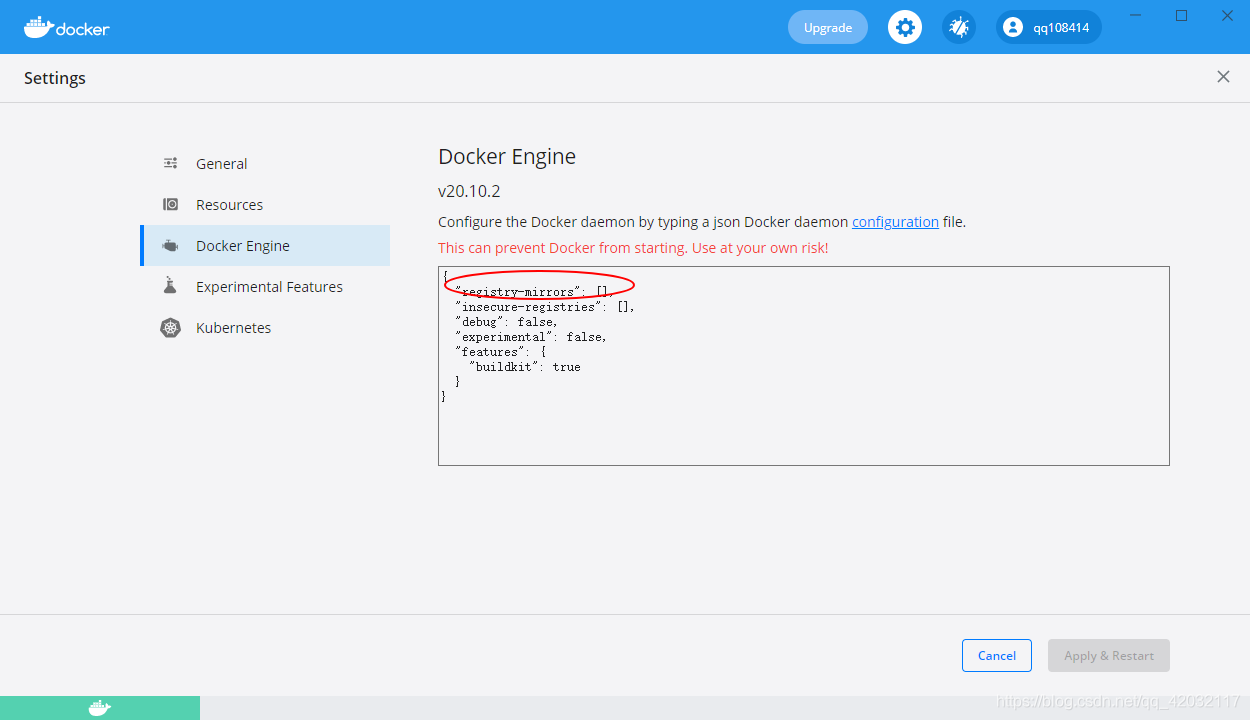
开始构建镜像
- 我们在E盘或者D盘创建一个WWW目录用于存放我们的项目
- 建议使用我这个地址 速度快的起飞。
cd wwwgit clone https://gitee.com/pltrue/laradockcd laradockcp env-example .envvim .env//修改文件mysql版本MYSQL_VERSION=5.7//需要开启swooleWORKSPACE_INSTALL_SWOOLE=truePHP_FPM_INSTALL_SWOOLE=truePHP_WORKER_INSTALL_SWOOLE=trueWORKSPACE_INSTALL_SWOOLE=true//开始拉取需要的镜像 完成之后继续下一步 docker-compose build nginx php-fpm redis mysql //启动容器 docker-composer up -d nginx php-fpm redis mysql//进入某个容器winpty docker-composer exec redis bash //windows git下 记得带上命令 winpty//进入主容器 winpty docker-composer exec workspace bash//www 映射的是本地 laradock 同级目录 所有的项目都在/var/www 目录下面cd /var/www/
配置项目 nginx
- 在laradock/nginx/sites目录下配置nginx配置文件 php框架的模板都有
//配置好了之后,重启nginxwinpty docker-composer exec nginx bashnginx -s reload
- 注意 laradock容器之间通信不能通过127.0.0.1 而是通过名:例如:host:redis host:mysql
- 如果需要配置额外的端口与容器通信 在docker-compose.yml、和env中配置新端口 然后重新重建容器
- 之后所有操作都一样。其他具体可以查看官方文档。有问题,在本文下面提出,我会即时答复。
转载地址:http://mywaz.baihongyu.com/
你可能感兴趣的文章